Chapter 0Essence of linear algebra preview

"There is hardly any theory which is more elementary than linear algebra, in spite of the fact that generations of professors and textbook writers have obscured its simplicity by preposterous calculations with matrices."

- Dieudonné

About the series

Linear algebra is used in almost every technical discipline in science and technology, yet it's also generally poorly understood by students taking it for the first time. A student might go through a class and learn how to compute things like matrix multiplication, determinants, cross products, and eigenvalues, yet come out without really understanding why matrix multiplication is defined the way it is, how the cross product is related to the determinant, or what eigenvalues really represent.

Oftentimes, students end up well-practiced in the numerical operations of matrices but are only vaguely aware of the geometric intuitions underlying it all. Each has its place, but roughly speaking, the geometric understanding is what lets you judge which tools to use for specific problems, feel why they work, and know how to interpret the results, while the numeric understanding let's you actually carry through the application of those tools.

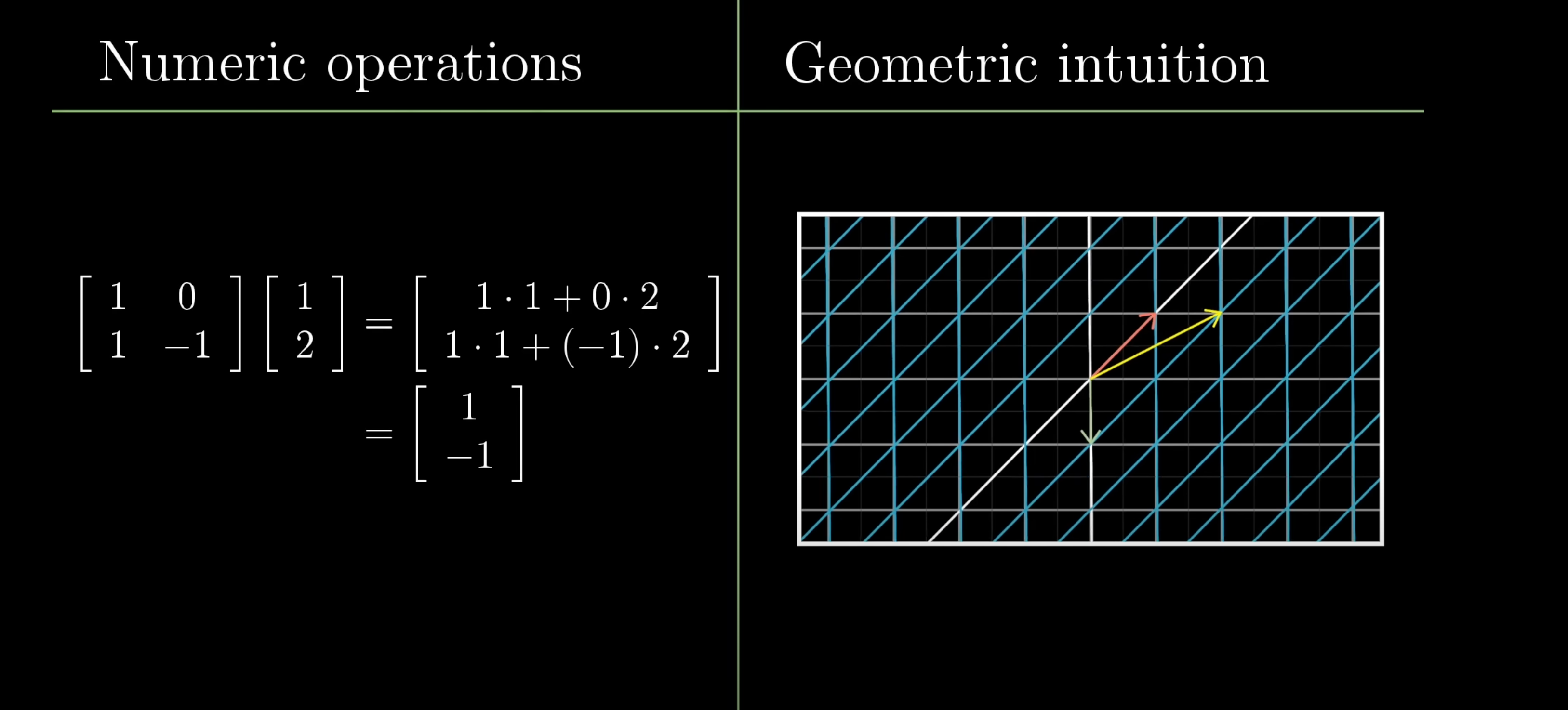
If you learn linear algebra without a solid geometric understanding, the problems can go unnoticed until you've gone much deeper into whatever field you happen to pursue, whether it's computer science, engineering, statistics, economics, or pure math. At that stage, if your class or job assumes fluency with linear algebra, the way that your professors or coworkers draw on their visual intuition to pull out the right tool can seem like unattainable wizardry if it looks like they're actually crunching all the numbers in their head for the operations they bring up.

Trigonometry analogy

As an analogy, imagine that when you first learned about the sine function in trigonometry, you were only shown this infinite polynomial. Which, by the way, is how your calculator defines the sine function.

Typically this is something a student wouldn't see until a calculus class, presumably when they've already built a relationship with what the sine function is, but in principle it would be perfectly valid to define the sine function formally this way from the start. It would just be a terrible idea pedagogically. Imagine in this hypothetical class that for homework, students were asked to practice computing approximations of the sine function by plugging in various numbers to this formula...

This class may have provided a vague idea that the sine function was supposed to be related to triangles, but it was never made clear exactly how this was the case because that was not the focus of the course.

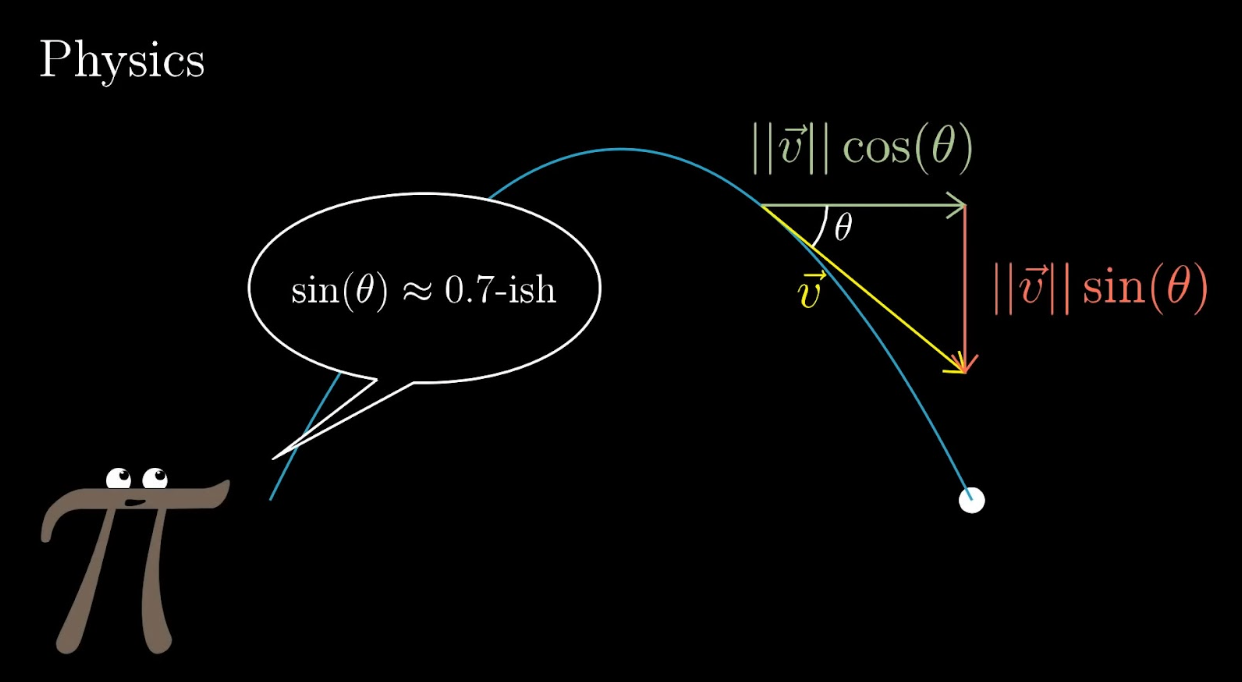
Later on, you find yourself in a physics course, where sines and cosines are thrown around left and right. People are able to tell immediately how to apply them and roughly approximate what the sine of a certain value will be. This would be pretty intimidating, wouldn't it? It would make it seem like the only people who are cut out for physics are those with computers for brains, and you would feel unduly slow or frustrating for taking so much longer on each problem.

It's not that different with linear algebra. Luckily, just as with trigonometry, there are a handful of intuitions, visual intuitions, underlying much of the subject.

How we'll approach this series

Unlike the trigonometry example, the connection between the computation and the visual intuition behind topics like matrix multiplication, determinants, eigenvalues and the rest are pretty straightforward. When you digest these and really understand how they relate to the corresponding numerical operations, the details of the subject, as well as how it is used in practice, start to feel a lot more reasonable.

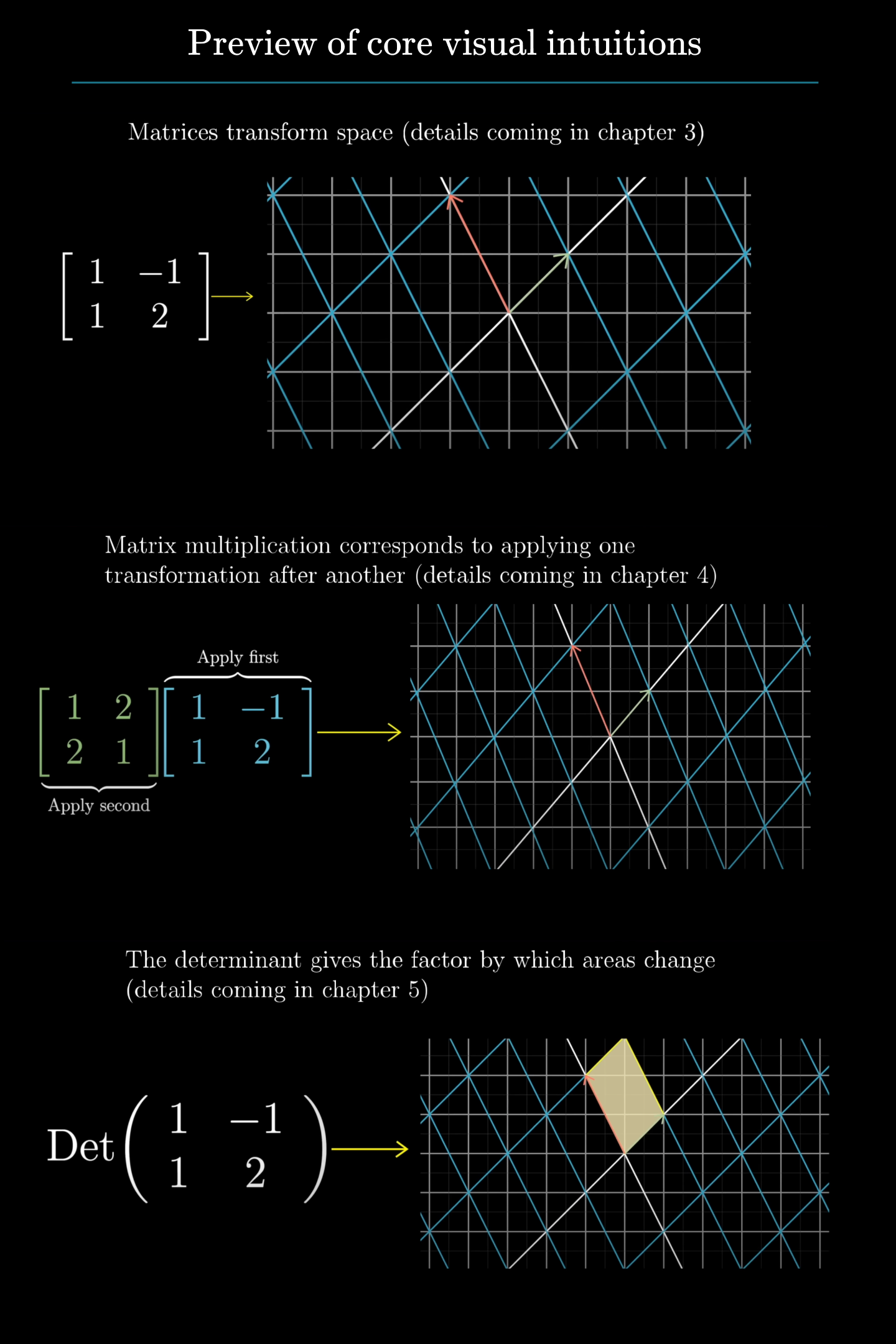
In fairness, most professors do make an effort to convey the geometric underpinnings of linear algebra, the sine example is admittedly extreme, but I do think many courses have students spending a disproportionate time on the numerical side, especially given that in this day and age we almost always get computers to handle that half leaving humans to worry about the conceptual half.

The goal of this series is to illustrate that conceptual half, from the basics of vectors, up through the core topics that make up the essence of linear algebra. The goal is not to teach the entirety of linear algebra, but to lay down all the right intuitions so that the learning you do moving forward is as productive and fruitful as it can be. I also hope this can be a resource for educators teaching courses that assume fluency with linear algebra, giving them a place to direct students who need that brush up.

So with that, in the next lesson, let's start at the beginning: What is a vector, exactly?